I. Inleiding
Water Kan Kerse Aansteek, Is Dit Waar? Dis Waar!
Is dit waar dat slange bang is vir edelgar? Dit is vals!
Wat ons vandag gaan bespreek, is:
Interferensie kan meet akkuraatheid verbeter, is dit waar?
Onder normale omstandighede is interferensie die natuurlike vyand van meting. Interferensie sal meetnauwkeurigheid verminder. In ernstige gevalle sal meting nie normaalweg uitgevoer word nie. Vanuit hierdie perspektief kan interferensie meetnauwkeurigheid verbeter, wat vals is!
Is dit egter altyd die geval? Is daar 'n situasie waar interferensie nie die meetnauwkeurigheid verminder nie, maar dit eerder verbeter?
Die antwoord is ja!
2. Inmengingsooreenkoms
Gekombineer met die werklike situasie, maak ons die volgende ooreenkoms oor die inmenging:
- Interferensie bevat nie GS-komponente nie. In die werklike meting is die interferensie hoofsaaklik WS-interferensie, en hierdie aanname is redelik.
- In vergelyking met die gemete GS-spanning, is die amplitude van interferensie relatief klein. Dit stem ooreen met die werklike situasie.
- Interferensie is 'n periodieke sein, of die gemiddelde waarde is nul binne 'n vaste tydperk. Hierdie punt is nie noodwendig waar in werklike meting nie. Aangesien die interferensie egter gewoonlik 'n hoërfrekwensie-WS-sein is, is die konvensie van nul gemiddelde vir die meeste interferensies redelik vir 'n langer tydperk.
3. Meetnauwkeurigheid onder interferensie
Die meeste elektriese meetinstrumente en meters gebruik nou AD-omsetters, en hul meetnauwkeurigheid is nou verwant aan die resolusie van die AD-omsetter. Oor die algemeen het AD-omsetters met hoër resolusie hoër meetnauwkeurigheid.
Die resolusie van AD is egter altyd beperk. As ons aanvaar dat die resolusie van AD 3 bisse is en die hoogste meetspanning 8V is, is die AD-omskakelaar gelykstaande aan 'n skaal wat in 8 dele verdeel is, elke deel is 1V. is 1V. Die meetresultaat van hierdie AD is altyd 'n heelgetal, en die desimale deel word altyd gedra of weggegooi, wat in hierdie artikel as gedra aanvaar word. Dra of weggooi sal meetfoute veroorsaak. Byvoorbeeld, 6.3V is groter as 6V en minder as 7V. Die AD-meetresultaat is 7V, en daar is 'n fout van 0.7V. Ons noem hierdie fout AD-kwantiseringsfout.
Vir die gerief van analise neem ons aan dat die skaal (AD-omskakelaar) geen ander meetfoute het behalwe die AD-kwantiseringsfout nie.
Nou gebruik ons twee identiese skale om die twee GS-spannings wat in Figuur 1 getoon word, sonder interferensie (ideale situasie) en met interferensie te meet.
Soos getoon in Figuur 1, is die werklike gemete GS-spanning 6.3V, en die GS-spanning in die linkerfiguur het geen interferensie nie, en dit is 'n konstante waarde in waarde. Die figuur aan die regterkant toon die gelykstroom wat deur die wisselstroom versteur word, en daar is 'n sekere fluktuasie in die waarde. Die GS-spanning in die regterdiagram is gelyk aan die GS-spanning in die linkerdiagram na die uitskakeling van die interferensiesein. Die rooi vierkant in die figuur verteenwoordig die omskakelingsresultaat van die AD-omskakelaar.

Ideale GS-spanning sonder interferensie
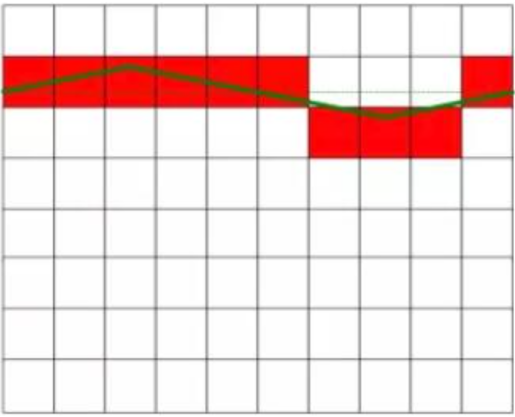
Pas 'n interfererende GS-spanning met 'n gemiddelde waarde van nul toe
Maak 10 metings van die gelykstroom in die twee gevalle in die bostaande figuur, en bereken dan die gemiddelde van die 10 metings.
Die eerste skaal aan die linkerkant word 10 keer gemeet, en die lesings is elke keer dieselfde. As gevolg van die invloed van die AD-kwantisasiefout, is elke lesing 7V. Nadat 10 metings gemiddeld is, is die resultaat steeds 7V. Die AD-kwantisasiefout is 0.7V, en die meetfout is 0.7V.
Die tweede skaal aan die regterkant het dramaties verander:
As gevolg van die verskil in die positiewe en negatiewe van die interferensiespanning en die amplitude, is die AD-kwantisasiefout verskillend by verskillende meetpunte. Onder die verandering van die AD-kwantisasiefout verander die AD-meetresultaat tussen 6V en 7V. Sewe van die metings was 7V, slegs drie was 6V, en die gemiddelde van die 10 metings was 6.3V! Die fout is 0V!
Trouens, geen fout is onmoontlik nie, want in die objektiewe wêreld is daar geen streng 6.3V nie! Daar is egter wel:
In die geval van geen interferensie nie, aangesien elke meetresultaat dieselfde is, bly die fout onveranderd na die gemiddeld van 10 metings!
Wanneer daar 'n gepaste hoeveelheid interferensie is, word die AD-kwantisasiefout met 'n orde van grootte verminder nadat 10 metings gemiddeld is! Die resolusie word met 'n orde van grootte verbeter! Die meetnauwkeurigheid word ook met 'n orde van grootte verbeter!
Die belangrikste vrae is:
Is dit dieselfde wanneer die gemete spanning ander waardes is?
Lesers kan die ooreenkoms oor interferensie in die tweede afdeling volg, die interferensie met 'n reeks numeriese waardes uitdruk, die interferensie op die gemete spanning superponeer, en dan die meetresultate van elke punt volgens die drabeginsel van die AD-omskakelaar bereken, en dan die gemiddelde waarde vir verifikasie bereken, solank die interferensie-amplitude die lesing na AD-kwantisering kan laat verander, en die monsterfrekwensie hoog genoeg is (veranderinge in interferensie-amplitude het 'n oorgangsproses, eerder as twee waardes van positief en negatief), en die akkuraatheid moet verbeter word!
Daar kan bewys word dat solank die gemete spanning nie presies 'n heelgetal is nie (dit bestaan nie in die objektiewe wêreld nie), daar 'n AD-kwantisasiefout sal wees, ongeag hoe groot die AD-kwantisasiefout is, solank die amplitude van die interferensie groter is as die AD-kwantisasiefout of groter as die minimum resolusie van AD, sal dit veroorsaak dat die meetresultaat tussen twee aangrensende waardes verander. Aangesien die interferensie positief en negatief simmetries is, is die grootte en waarskynlikheid van afname en toename gelyk. Daarom, wanneer die werklike waarde nader aan watter waarde is, is die waarskynlikheid dat watter waarde sal verskyn groter, en dit sal naby aan watter waarde wees na gemiddelde berekening.
Dit wil sê: die gemiddelde waarde van veelvuldige metings (interferensiegemiddelde waarde is nul) moet nader aan die meetresultaat sonder interferensie wees, dit wil sê, die gebruik van die WS-interferensiesein met 'n gemiddelde waarde van nul en die gemiddelde van veelvuldige metings kan die ekwivalente AD-kwantiseringsfoute verminder, die AD-metingsresolusie verbeter en die metingsakkuraatheid verbeter!
Plasingstyd: 13 Julie 2023




